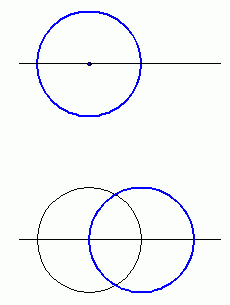Nic nigdy nie dzieje się przypadkowo, wszystko we wszechświecie ma sens, a każde zdarzenie bezpośrednio zależy od zdarzenia go poprzedzającego i samo w sobie stanowi bazę dla zdarzenia następnego. Piktogramy... Geometryczne twory - piękne i intrygujące i choć na całym świecie istnieje kilkanaście grup tworzących owe znaki w zbożu to są takie piktogramy których rekonstrukcji w zbożu nie podjęłaby się żadna grupa tzw. "circlemakerów", a jeśli nawet to finalny efekt byłby daleki od oryginału i to nie za sprawą różnic wizualnych ale za sprawą sporych różnic w geometrii konstrukcji.
Na świecie wyróżniono kilkanaście piktogramów co do których istnieje niemalże 100-procentowa pewność, że nie zostały wykonane przez ludzi... mało tego... uznano owe figury za niemożliwe do rekonstrukcji w zbożu w takiej formie jaką one przyjęły.
Zwolennicy teorii jakoby kręgi zbożowe tworzone były przez ludzi z deskami / walcami będą musieli przełknąć gorzką pigułkę po informacjach zawartych w tym temacie. Nawet mając do dyspozycji najlepszą grupę "circlemakerów" (weźmy chociażby ludzi z dużym doświadczeniem z circlemakers.org), nawet przy użyciu najlepszego sprzętu, noktowizorów, dalmierzy, nie można zrobić tego co przez ostatnie kilka lat miało miejsce głównie w Anglii ale również na całym świecie.
Przejdźmy do rzeczy
Badania kręgów zbożowych wykazują, że KAŻDY element stanowiący część piktogramu choćby był najmniejszy i najmniej ważny jest umiejscowiony w zbożu zgodnie ze ściśle określonymi regułami geometrycznymi. NIC nie dzieje się przypadkowo. Elementy te umiejscawiane są przy udziale bardzo restrykcyjnych reguł geometrii.
Weźmy dwa przykładowe piktogramy:
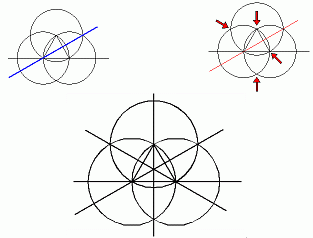
Pierwszy to piktogram który pojawił się w Winterbourne Bassett, nr. Avebury, Wiltshire, 2 czerwca 1997 roku. Nazwany został "Harlekin". Formacje tą bardzo łatwo wykreślić na papierze / komputerze ale... nie w zbożu! Po kilku krokach rekonstrukcyjnych mamy sytuacje pokazaną na rysunku niżej:
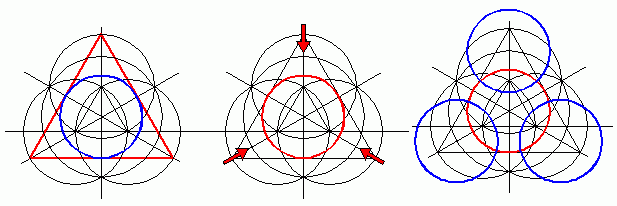
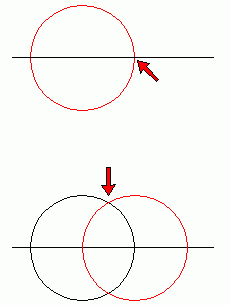
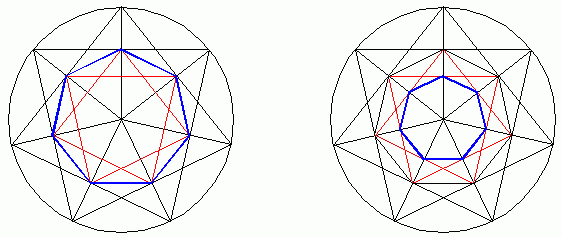
Widzimy kilkukrotne wykreślanie okręgów, okrąg centralny a następnie biorąc pod uwagę pewne punkty przecięcia wykreślamy trzy okręgi (niebieskie) które stanowić będą bazę dla dalszej konstrukcji. Zatem kolejne kroki..
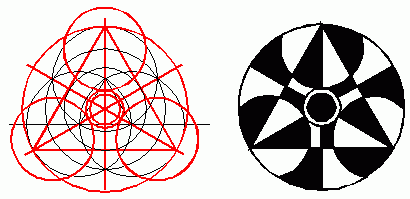
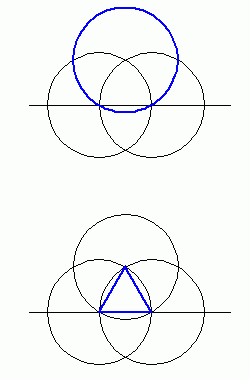
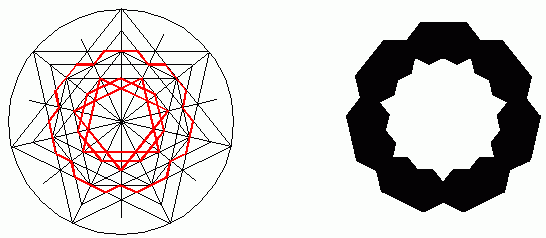
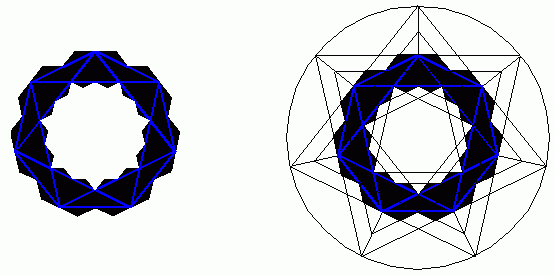
Kilka dodatkowych linii i okręgów i formacja gotowa. Widzimy wiele różnych elementów w finalnej konstrukcji które powstały tylko i wyłącznie na podstawie kroków przeprowadzonych wcześniej (zasady geometrii i wykreślania). Następnie dostrzegamy wiele konstrukcyjnych elementów które nie są obecne w formie finalnej a MUSIAŁY być wcześniej wykreślone bo stanowią bazę na jakiej opiera się forma końcowa. Weźmy chociażby pod uwagę duży okrąg (granice którego oznaczono trzema czerwonymi strzałkami)
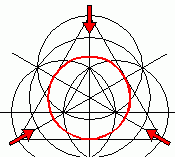
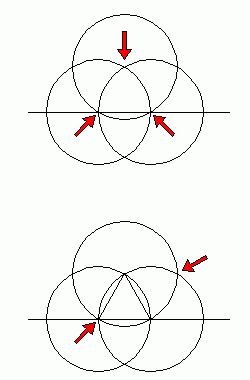
Okrąg ten MUSIAŁ być wykreślony bo dzięki niemu można było rozlokować trzy niebieskie (na rysunku) okręgi których środki stanowią przecięcie właśnie owego dużego okręgu z liniami. Czy widzicie gdzieś na konstrukcji finalnej jakikolwiek ślad owego dużego okręgu?
Mało tego... naukowo udowodniono, że rozmiar trzech czerwonych okręgów (na marginesie określony przez czerwony trójkąt) w stosunku do rozmiaru całej formacji wyrażany jest stosunkiem diatonicznym (oktawy). Nie jest to coś przypadkowego, to logika geometrii.
Weźmy teraz pod uwagę inną formację która pojawiła się w Barbury Castle w 1999 roku a nazwana została "Półksiężyce".
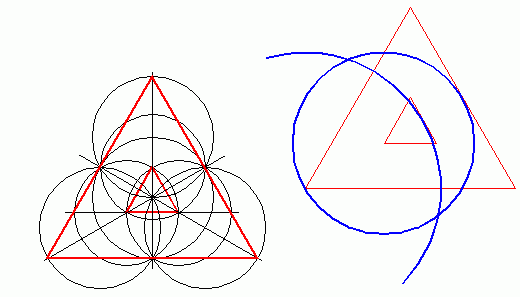
Pierwszy diagram powyżej pokazuje konstrukcję po paru podstawowych krokach. Mały trójkąt i duży po raz kolejny tworzą stosunek diatoniczny. Aby uformować "półksiężyce" należy wykreślić dwa okręgi. Pierwszy z centrum w lewym dolnym rogu dużego trójkąta tak aby łuk ledwo dotykał ściany małego trójkąta. Teraz odwrotna sytuacja. Konstrukcja okręgu w lewym dolnym rogu małego trójkąta tak aby łuk ledwo dotykał ściany dużego trójkąta. Te dwa okręgi nałożone na siebie formułują półksiężyc. Półksiężyc ten jest dokładnie tego samego rozmiaru i kształtu jak ten znaleziony w formacji z Barbury Castle.

Znów widzimy potrzebne elementy jakich nie można znaleźć w formacji finalnej. Dwa trójkąty są absolutnie niezbędne do stworzenia półksiężycy ale nie ma ich w konstrukcji końcowej, jak zatem w sposób perfekcyjny wykonano te figury? Wszystko to można zrobić na papierze ale nie w zbożu.
Wiele osób podaje argumenty... przecież konstrukcje tego typu można wykonać na papierze, zmierzyć odpowiednie odległości między punktami, wziąć kilkanaście osób, linki, taśmy, słupki i wykonać od razu efekt finalny bez wykreślania. Owszem można i tak właśnie robią to circlemakerzy. Najpierw rysują oni formacje na papierze, wykreślają ją geometrycznie. Następnie wykorzystując istniejące w zbożu ścieżki wyznaczają punkty krytyczne (kontrolne) od których będą mierzone poszczególne odległości i które to stanowić mają punkty odniesienia. Tak właśnie to wygląda jednakże kiedy w przypadku kręgów prawdziwych geometria jest dokładna co do milimetra, kąty są zachowane to w przypadku kręgów wykonanych przez ludzi mamy do czynienia ze sporymi odstępstwami od zamierzonego efektu i choć tych "małych" różnic na pierwszy rzut oka nie widać to przy nałożeniu siatki geometrycznej na figurę widać spore różnice. Są też takie piktogramy których NIE DA się zrobić nawet gdybyśmy mieli zaczynać prace od konstrukcji finalnej ale o tym w kolejnej części.
Podsumujmy teraz parę faktów:
- Wielkość i umiejscowienie elementów w formacji zbożowej nie jest przypadkowe i podlega ściśle zasadom geometrii.
- Ponieważ stosujemy geometrię i wykreślanie, wiele elementów posiada tzw. stosunek diatoniczny wobec innych elementów.
- Wiele z koniecznych elementów konstrukcyjnych nie może być znalezione w formacjach finalnych (można wygumować na papierze ale nie można podnieść w górę raz położonych kłosów).
Autor: Eurycide
wykorzystano zdjęcia ze strony: http://cropcirclecon.../bert2000a.html
C.D.N