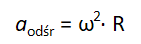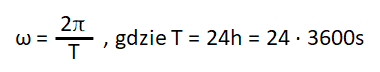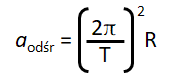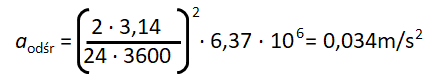7696 replies to this topic

[Staniq]

... nie widziałem by smuga kondensacyjna pojawiała się i znikała, była poprzerywana za samolotem. NIGDY!

Pewnie szukałeś drobnych na chodniku, które ktoś zgubił.

Tobie można tłumaczyć, a i tak nie zrozumiesz. 

 

 

Mam już dosyć tego tematu. To jest mój  jeden z ostatnich wpisów na tym forum. Mam nadzieję że prawda zwycięży, że my Polacy wstaniemy z kolan i zawalczymy o lepszą przyszłość dla naszych dzieci, wnuków, i prawnuków. Żegnam Was, odbijam od tematu i niech się dzieje wola boża.

Ciekawe ile jeszcze tych ostatnich wpisów będzie.

 

 

5g to jest nasza ostatnia linia oporu. Zaakceptujecie to gie, to naprawdę nic już Wam nie pomoże.

Nie masz nawet bladego pojęcia o technologii, więc nie zabieraj głosu. WiFi też Ci szkodzi, co zresztą widzimy. Może HiFi też jest szkodliwe...

[Ogarnięty]

Staniq Ty wierzysz w oficjalną wersję 911, 5G dla Ciebie jest bezpieczne, piszesz w każdym poście wierutne bzdury, robisz wycieczki osobiste, obrażasz. Dla mnie jako dyskutant jesteś skończony. Nie obraź się ale od teraz będę najzwyczajniej zlewał Twoje nic nie wnoszące wypociny. 

 

[Panjuzek]

Up@

 

piszesz w każdym poście wierutne bzdury,

Ciebie panie @ogarnięty, jeśli chodzi o bzdury, nic nie przebije.

 

 

robisz wycieczki osobiste, obrażasz.Dla mnie jako dyskutant jesteś skończony.

 Problem polega na tym że mierzysz innych swoją miarą i przypisujesz im Swoje przywary.

 

 

5G dla Ciebie jest bezpieczne,

 

Na 100% jestem pewien że nie ogarniasz różnicy pomiędzy 5g i 4g.  Jak zwykle łykasz odchody pozostawione, przez niezbyt ogarniętych youtuberów, i popijasz je mgięłką z wyimaginowanych chemitrailsów. Czas dorosnąć.

[Ogarnięty]

Haha tak jak myślałem, po 911, globalnym ociepleniu, chemtrails, teraz nasi totalnie "zwykli użytkownicy", nasi "sceptycy", którzy nie działają, jako zorganizowana grupa rozdająca sobie nawzajem nagrody i plusiki, BĘDĄ BRONIĆ 5G!! I oni w ogóle nie są pieskami systemu, wynajętymi do ogłupiania ludzi! Jak tak myślisz, to wróć do szkoły nieuku jeden, w której o trollach, dezinformatorach, zbrodniczych elitach, eskimosach nie było żadnej lekcji! Dorośnijmy więc i łykajmy te ich wszystkie bzdury i kłamstwa! Mamy być bydłem, debilami, motłochem, dla którego system już dawno wyznaczył rolę i miejsce w szeregu... 

[Wszystko]

Mocne słowa jak na kogoś, kto wierzy, że Ziemia jest płaska.

Poza tym powstrzymajcie się od schodzenia do coraz niższego poziomu. Sformułowania typu łykasz odchody, nieuku jeden, psychicznie chory, to prymitywizm i nie są zbyt wysokich lotów.
Więc prośba dotyczy przede wszystkim ogarniętego a reszta niech się domyśli o kogo chodzi.
Aha i temat ma mało wspólnego z 5g i 11/9 więc nie uciekaj w bok na poboczne ścieżki.

[Staniq]

Staniq Ty wierzysz w oficjalną wersję 911, 5G dla Ciebie jest bezpieczne, piszesz w każdym poście wierutne bzdury, robisz wycieczki osobiste, obrażasz.

W 911 nigdy nie napisałem nic, co mijałoby się z prawdą. Zadałem Ci kiedyś pytanie, czy jesteś w stanie podważyć temperatury spalania paliwa i temperatury utraty swoich właściwości dla stali konstrukcyjnej. Nigdy nie odpowiedziałeś, posługujesz się tylko ogólnikami, bo nawet w internecie nie potrafisz znaleźć materiałów. Nie potrafisz odpowiedzieć wprost na żadne zadane Ci w tym i w innych tematach pytanie.

Skoro sam nie potrafisz zrozumieć, zapewne myślisz, że inni też nie potrafią. Błąd, bo my nie udajemy kogoś, kim nie jesteśmy.

Tak nawiasem, nie znam nikogo (a mam sporą grupę znajomych którzy ukończyli różne studia) z wykształceniem wyższym, kto używałby tak ubogiego i prymitywnego  słownictwa jak Twoje. Koleżanka po socjologii miała dość (nazwijmy to) "swobodne" zdanie na Twój temat, ale nie nadaje się to do zacytowania. 

Drogi panie "adwokacie" to nie jest dno, Pan grzebiesz w mule i to głęboko. Nie wiesz i nie rozumiesz co to jest 3G,4G,5G, nie rozumiesz promieniowania elektromagnetycznego i fizyki na podstawowym poziomie. Do szkoły sam powinieneś wrócić, a nie wysyłać tam innych.

Pewnie kury przestały Ci się nieść i krowy straciły mleko. Mówię Ci, na HiFi też uważaj, bo może być gorsze od WiFi...

[Ogarnięty]

up

W 911 nigdy nie napisałem nic, co mijałoby się z prawdą. Zadałem Ci kiedyś pytanie, czy jesteś w stanie podważyć temperatury spalania paliwa i temperatury utraty swoich właściwości dla stali konstrukcyjnej.

A czy dla Ciebie znawco praw fizyki możliwe jest by dwie potężne wierze zamieniły się w .... proszek? Proszę Cię odpuść sobie, bo walisz sobie po koanach z bazooki. 

 

Błąd, bo my nie udajemy kogoś, kim nie jesteśmy.

 

No wiem, że nie udajecie. Normalni użytkownicy doskonale rozumieją kim jesteście i jakie jest Wasze tutaj i na innych miejscach w sieci zadanie. 

 

Reszta wypowiedzi to ponowne obrażanie. Spójrz na swoje słownictwo i kompletnie nic nie wnoszące do dyskusji posty. Merytorycznie jesteś strasznie marny. Mało wiesz i jeszcze gorzej to minimum wiedzy przedstawiasz.

 

Wszystko

Aha i temat ma mało wspólnego z 5g i 11/9 więc nie uciekaj w bok na poboczne ścieżki.

Temat ma mnóstwo wspólnego z 911 i 5G. 911 - jedno wielkie kłamstwo i naplucie w twarz miliardom ludzi na całym świecie - dowód na istnienie globalnego spisku, do dzisiaj nie rozliczona zbrodnia, o której nikt z elit nie mówi, w tym  nasi wynajęci aktorzy aka politycy. To, że ludzie nic z tym nie zrobili rozzuchwaliło zbrodnicze elity, że mogą spokojnie przeprowadzić przez lata akcję opryskiwania ludzi. A i to trwa w najlepsze, więc nic nie stoi na przeszkodzie by usmażyć ludzi technologią 5G, dla której działania chemtrails jest konieczne. Zbrodniarze działają, zabijają, trują, a ludzie dalej smacznie sobie śpią. We Francji się ruszyło, ale kiedy reszta świata w końcu pogoni to towarzystwo? 

[Zaciekawiony]

Wieże nie zamieniły się w proszek, z gruzowiska ściągnięto setki ton stalowych belek.

Użytkownik Zaciekawiony edytował ten post 13.03.2019 - 19:31

[Wszystko]

Czyli wychodzi na to że opryskiwanie ludzi chemtrailsami nie przynosi zamierzonych efektów bo populacja światowa nadal rośnie więc wymyślono nową technologię 5g do smażenia ludzi. Tylko ciekawe jak to smażenie będzie wyglądać czy na oleju, oliwie, maśle?

Wg mnie opryskiwanie ludzi niewiele daje właśnie dlatego że Ziemia jest płaska i większość z tych oprysków spada poza krawędź planety. Co o tym myślisz?

[Ogarnięty]

Wszystko 

No i połączyliśmy wszystkie te w/wymienione tematy z płaską Ziemią... OK! Skoro ziemia obraca się wokół własnej osi z prędkością około 1667  km/h https://pl.wikipedia..._obrotowy_Ziemi, a prędkość maksymalna typowego samolotu pasażerskiego wynosi 876 km/h https://pl.wikipedia...wiki/Boeing_737 to jakim cudem samolot lecący w tym samym kierunku co ruch obrotowy Ziemi ma szansę dolecieć do celu, który będzie się oddalał od samolotu z.... dwukrotnie (sic!) większa prędkością! Nadal wierzysz że Ziemia to obracająca się kulka?

 

Tyle o płaskiej Ziemi i tyle w temacie jak łatwo jest ogłupić ludzi, którzy nie poświęcają ani chwili by zweryfikować serwowane im od dziecka wierutne kłamstwa na wiele, wiele tematów. Tak samo było i jest z kształtem Ziemi, 911, chemtrails, a teraz z 5G. 

Użytkownik Ogarnięty edytował ten post 13.03.2019 - 20:06

[Staniq]

...więc nic nie stoi na przeszkodzie by usmażyć ludzi technologią 5G, dla której działania chemtrails jest konieczne. 

Pewnie mikrofalówki nie zamknąłeś, stąd te problemy ze zrozumieniem.

 

Brak merytoryki widać i to na podstawowym poziomie tutaj:

A czy dla Ciebie znawco praw fizyki możliwe jest by dwie potężne wierze zamieniły się w .... proszek?

Nie, bo:

 

Wieże nie zamieniły się w proszek, z gruzowiska ściągnięto setki ton stalowych belek.

Merytoryczna wypowiedź wygląda tak jak wyżej.

 

A teraz wiedza...

 Merytorycznie jesteś strasznie marny. Mało wiesz i jeszcze gorzej to minimum wiedzy przedstawiasz.

Cóż, alfą i omegą nie jestem, ale w dalszym ciągu nie odpowiedziałeś na kilka pytań, do których podstawy fizyki poznałeś w podstawówce i rozszerzyłeś w szkole średniej lub zawodowej. Jeżeli tych podstaw nie znasz lub nie rozumiesz, znaczy to dobitnie, żeś nawet podstawówki nie ukończył, a jeżeli Ci się to udało, to pani od fizyki musiała mieć dobry dzień. Cokolwiek byś nie powiedział o swoim wykształceniu, negowanie podstaw fizyki przeczy temu wyraźnie i nie jest to obraza, lecz stwierdzenie faktu. 

Właśnie przykład tych trzech tematów (911 i chemtrails, oraz płaskiej ziemi) jest wystarczający. Takiego ograniczenia jeszcze nie spotkałem. Zaprzeczając, nie potrafisz przedstawić żadnego kontrargumentu poza:

- wierutne kłamstwa

- jesteście ślepi

- agenci

- pieski systemu

- sruty tuty.

Niejednokrotnie proszono Cię o odpowiedzi i co? Totalna zlewka i bełkot za bełkotem. 

 

Taaak, a płaska ziemia leży na żółwiach...  Tyle lat trollować, że to Ci się nie znudziło?

[Panjuzek]

 

więc wymyślono nową technologię 5g do smażenia ludzi.

 

 No niezupełnie tak.  Grzebnąłem trochę w netach, i znalazłem związek pomiędzy opryskami i 5G. Jest petarda, po prostu wyższy poziom absurdu, spowodowany brakiem wiedzy a wręcz brakiem chęci jej zdobywania, aka @ogarnięty.

 

A więc jest tak: Produkowane są już procesory w technologii 10nm, na dniach wejdzie na rynek technologia 7nm, a za rok lub dwa być może nawet 5nm.

 I teraz najlepsze. Jakiś głąb, wykombinował sobie że skoro procesro jest produkowany w technologii powiedzmy 10nm, to oznacza że ten procesor bedzia miał właśnie taką wielkość

  No i powstała historia, że nano chipy, są lub będą zrzucane na ludzi przy pomocy chemitrails, dzięki czemu dostaną się do naszych organizmów, a 5G umożliwi wielkim tego świata totalną kontrolę  nad plebsem, poprzez łączenie się z tymi nano-chipami i dokonywanie różnego rodzaju niecnych czynów.

 

 Coś strasznego. Jak niewiedza, może robić kaszę z ludzkich mózgów.

 

P.S. Specjalnie dla @ogarniętego

 To że procesor jest zrobiony w technologii 10nm, 7nm czy nawet niedługo w 5nm, nie oznacza że jego wielkość wynosi 10 czy 7nm. Oznacza jedynie odległości pomiędzy poszczególnymi tranzystorami, będącymi elementami każdego chipa czy procesora będzie wynosiła właśnie 10 lub 7 nanometrów. W zasadzie to to te dwa określenie można zawrzeć w jednym, troszkę archaicznym: "układ scalony"

 Jeżeli czegoś nie zrozumiałeś z chęcią odpowiem na Twoje pytania, chociaż są na tym forum ludzie, którzy znają si ę na tym znacznie lepiej niż ja. W sumie to tylko stolarzem jestem, a agentura to taka fucha na boku.

 

edit

 

 

No i połączyliśmy wszystkie te w/wymienione tematy z płaską Ziemią... OK! Skoro ziemia obraca się wokół własnej osi z prędkością około 1667  km/h https://pl.wikipedia..._obrotowy_Ziemi, a prędkość maksymalna typowego samolotu pasażerskiego wynosi 876 km/h https://pl.wikipedia...wiki/Boeing_737 to jakim cudem samolot lecący w tym samym kierunku co ruch obrotowy Ziemi ma szansę dolecieć do celu, który będzie się oddalał od samolotu z.... dwukrotnie (sic!) większa prędkością! Nadal wierzysz że Ziemia to obracająca się kulka?

Ano takim cudem że samolot leci w masie powietrza, która porusza się razem z ziemią. gdyby atmosfera była nieruchoma i tyko ziemia kręciła by się z prędkością 1667km/h to na powierzchni mielibyśmy wiatry wiejące zawsze w jednym kierunku z prędkością 1667km/h, Jak ty podstawówkę dałeś radę skończyć? Czy nie dałeś?

Użytkownik Panjuzek edytował ten post 13.03.2019 - 20:39

[Ogarnięty]

Staniq

Nadal ZERO merytorycznych postów! Zero. Pokazuje Ci logiczny argument, że Ziemia się nie obraca, a Ty o żółwiach! To już nie działa. 

 

PanJuzek

Człowieku co za bzdury wypisujesz. Co to ma wszystko wspólnego z 5G to nawet Ty sam chyba nie wiesz. Widać wyraźnie, że dostaliście kolejne zlecenie, bronić kolejnej zbrodni elit - 5G. I będziecie znowu latami pilnowali odpowiednich tematów, tak by bydełko się nie obudziło, żyło w nieświadomości i spokojnie pozwalało się zatruwać i zabijać. Trochę już mi się rzygać chce rozmawiając z Wami. Muszę okazać Wam litość, bo za pół h Bayern Liverpool i nie chce mi się rozmawiać ze zwykłymi trolejbusami. 

[Staniq]

No to ujawniamy się? No dobra, ja jestem też agentem i siedzę jak Panjuzek w UK bo trudniej mnie tutaj wyśledzić. 

Weźcie się ujawnijcie, Quintus nie będzie się musiał domyślać "who is who".

Od razu mi lepiej jak się ujawniłem.

 

up@

To Ty nie wiesz o tym, że ziemia jest wsparta na żółwiach? Brak Ci podstawowej wiedzy o płaskiej ziemi, a bierzesz się za dyskusję.

 

Dobra, Twój z tyłka wyjęty argument o problemie prędkości obrotowej ziemi.

Ziemia, to nie karuzela, więc argument błędny, ale...

Aby jednak mieć stuprocentową pewność, najlepiej jest policzyć, jaka siła odśrodkowa panuje na równiku i jak ma się ona do siły przyciągania ziemskiego. Dla wygody obliczeń lepiej jednak będzie porównać przyspieszenia, przede wszystkim dlatego, że przyspieszenie ziemskie związane z siłą przyciągania jest stałe (g = 9,81m/s2), a także dlatego, że licząc siłę konieczne byłoby ustalenie masy ciała, na które ona działa (bo siła to wszak masa razy przyspieszenie – F = m·a). Dodatkowo obliczenia można uprościć zastępując prędkość liniową prędkością kątową, czyli prędkością z jaką Ziemia obraca się o zadany kąt. Wzór na przyspieszenie odśrodkowe zależne od prędkości kątowej wygląda tak:

 

                                            

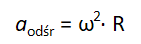
przy czym:

 

                                             

 

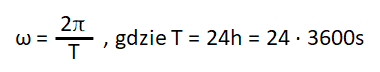
więc:

 

                                             

 

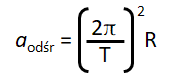
Podstawiając powyższe do wzoru wraz z wartością promienia Ziemi tj. R = 6,37 · 106m, otrzymamy wynik:

 

                                             

 

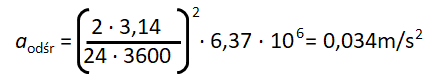
Przyjmując na chwilę przybliżoną wartość przyspieszenia ziemskiego, tj. g = 10m/s2 widać, że otrzymany wynik to ledwie 0,3% tego przyspieszenia (zaokrąglając 0,034 do 0,03). Odejmując zaś wartość przyspieszenia odśrodkowego od przyspieszenia ziemskiego, okaże się, że na równiku zmniejsza się ono z 9,81m/s2 do 9,79m/s2

Jaki z tego wniosek? Ano taki, aby nie wsiadać bezwiednie na karuzelę wątpliwej analogii i w ten sposób dawać sobie zawrócić w głowie. Siła odśrodkowa ruchu wirowego Ziemi z punktu widzenia siły jej przyciągania grawitacyjnego, nie ma praktycznie znaczenia.

 

Zatem płaskoziemcy argument do bani. No tak, zapomniałem... przecież matematyka i fizyka kłamie.

[Panjuzek]

 

Człowieku co za bzdury wypisujesz. Co to ma wszystko wspólnego z 5G

 To może wyjaśnisz nam łaskawie jaki związek z chemitrailsami ma 5G? pisałeś o tym niedawno. Chyba nie muszę cytować?

 

 

Pokazuje Ci logiczny argument, że Ziemia się nie obraca

 Ani to argument ani logiczny.

Użytkownik Panjuzek edytował ten post 13.03.2019 - 20:44