... czyli jak Wielka Piramida z kosmicznego "nie wiadomo czego" staje się najzwyklejszym egipskim grobowcem.
Autor: mariush
Początkowo ten post miał być po prostu odpowiedzią na jeden z postów sugerujących tajemniczą matematyczno-astronomiczną numerologię ukrytą w piramidzie Chufu. Jednak stwierdziłem ostatecznie, że może on być samodzielnym tematem i tym też on się ostatecznie stał.
Przyjrzałem się w nim i zanalizowałem niemal wszystkie (a na pewno wszystkie najważniejsze) argumenty, które mają świadczyć za zaawansowaną wiedzą jaką kryją wymiary oraz położenie geograficzne wyjątkowo słynnej (między innymi z tego powodu) Wielkiej Piramidy Chufu. Mam nadzieję, że ten post nie przejdzie niezauważony, a będzie przedmiotem ożywionej dyskusji. Ja ze swojej strony będę się starał odpowiedzieć na wszelkie ewentualne pytania...
Zacznę od rzeczy, które do odrzucenia nie wymagają użycia żadnego aparatu matematycznego.
Nic w tym nadzwyczajnego. Określenie kierunku N-S jest dziecinnie proste i Egipcjanie dobrze o tym wiedzieli. Wystarczy wbić w ziemię pręt (gnomon) i wraz z upływem dnia obserwować zmianę jego cienia. Położenie, w którym ma on najkrótszą długość wyznacza szukany kierunek.Piramida stoi prawie dokładnie na osi Północ-Południe.
Przy okazji wyjaśnię dużą dokładność wyznaczenia kątów prostych piramidy. Egipcjanie wiedzieli i to od dawna, że trójkąt o bokach długości 3, 4, 5 jest prostokątny. Swoją drogą jego zwyczajowa nazwa to trójkąt egipski. :smile: Za pomocą tej prostej konstrukcji architekci wyznaczali kąty proste w terenie.
Nieprawda. Wystarczy wziąść atlas i zerknąć na mapę świata (najlepiej w odwzorowaniu walcowym równoodległościowym południkowo) żeby się o tym przekonać. Zresztą...Południk biegnący przez piramidę jest najdłuższym biegnącym przez ląd.
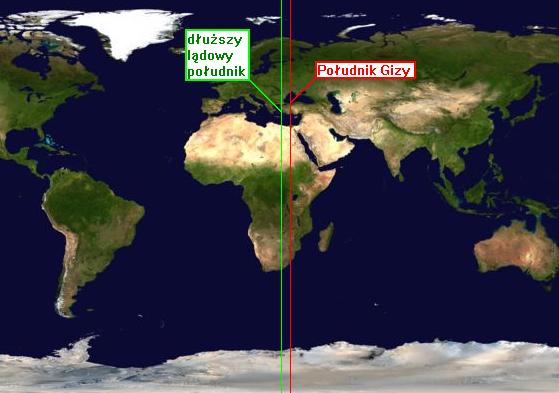
Bez sensu. Delta rzeczna to bardzo dynamiczny twór. Delta Nilu przyrasta o ok. 12 m rocznie. Na przestrzeni 4500 lat przyrosła więc o ok. 50 km. To mniej więcej 1/3 jej obecnych rozmiarów. Tak przy okazji: Rozmiar delty Nilu odpowiada kumulacji osadów przez ok. 13 000 lat, czyli mniej więcej czasowi od zakończenia się ostatniego zlodowacenia.Kąty piramidy dzielą Deltę Nilu na dwie równe części.
I co w tym nadzwyczajnego? Ja też jeśli pochylę się odpowiednio w stronę Słońca, to też nie będę rzucał cienia. Piramida ma pochyłe ściany, więc w pewnych (raczej cieplejszych) porach roku i o pewnych porach dnia (nawet poza południem) nie będzie rzucać cienia.Piramida od końca lutego do połowy października nie rzuca w południe żadnego cienia.
Cytuję za jedną z paranormalnych stron:Piramida jest zegarem słonecznym, pokazującym pory i długość roku.
Wydaje się też, że Wielka Piramida mogła być wykorzystywana jako kalendarz i zegar słoneczny. Podczas równonocy jesiennej, w porze dnia, gdy słońce osiąga najwyższy punkt na niebie, Wielka Piramida rzuca cień na rozciągającą się przed nią wielką północną terasę. Aż do chwili przesilenia zimowego cień ten z każdym dniem wydłuża się coraz bardziej i temu przyrostowi długosci odpowiada długość kolejnych, kamiennych płyt terasy. W ten sposób Piramida spełnia rolę nadzwyczaj precyzyjnego kalendarza.
To zwykła nadinterpretacja. Każde dziecko wie, że długość cienia każdego oświetlonego przez Słońce przedmiotu zależy od pory dnia i roku. Nie trzeba budowania 150-metrowej piramidy, aby ten fakt wykorzystać. Egipcjanie też o tym wiedzieli i realizowali swoje zegary i kalendarze słoneczne w o wiele prostszy sposób. Tak przy okazji chciałbym zobaczyć te terasy, które rzekomo określają pory roku.
Długośc piramidy??? :surprised: Jak mi to ktoś przetłumaczy na polski, to postaram się w tej kwestii wypowiedzieć.Stosunek długości i objętości piramidy odpowiada stosunkowi promienia do powierzchni koła.
Teraz niestety bez prostych obliczeń się nie obejdzie... :-D
Nieprawda. Jest spory problem z wartością wysokości piramidy. Fakt ten wynika z trudności jej pomiaru w porównaniu np. z pomiarem długości podstawy. Znalazłem wiele różnych wartości oscylujących głównie między 146 a 147 metrów. Wybrałem wynik powtarzający się najczęściej, a jako jego błąd przyjąłem wartość odpowiadająca jego rozbieżności w stosunku do ok. 75 % pozostałych wyników.Wysokość piramidy razy 10 do dziewiątej potęgi (miliard) jest równa średniej odległości Ziemi od Słońca.
Wysokość piramidy: 146, 64 ± 0, 20 m
Zgodnie z "piramidalnym przepisem" średnia odległość Ziemia-Słońce powinna wynosić: r = 146, 64 ± 0, 20 mln km.
Tymczasem prawdziwa średnia odległość Z-S wynosi 149, 6 mln km. To błąd rzędu 2 %. To wyjątkowo dużo jak na precyzję egipskich budowniczych. Wspomnę przy okazji, że dla starożytnych Egipcjan milion był największą rozważaną liczbą i zapisów większych wartości raczej próżno szukać.
Bzdura. Łokieć egipski (królewski) to ok. 0, 524 m i długość boku piramidy w tych jednostkach wynosi 440. Tak nawiasem, od kiedy długość roku słonecznego zależy od położenia na kuli ziemskiej??? :surprised:Długość boku podstawy wynosi 365,342 łokci egipskich i jest równa liczbie dni roku słonecznego w tropikach.
Nieprawda. Szerokość geograficzna piramidy Chufu wynosi : 29°58.8' N. Odległość kątowa od bieguna N wynosi więc:Odległość do bieguna N jest równa odległości do środka Ziemi i odległości od bieguna do środka Ziemi.
90° - 29°58.8' = 60°01.2'
Dane Ziemi: (model elipsoidy GRS-80)
Średni promień równikowy = 6 378, 137 km
Średni promień biegunowy = 6 356, 752 km
Obwód Ziemi południkowy = 40 007, 863 km
Łuk 60°01.2' to 0, 1667 pełnego kąta 360° . Taką samą część obwodu południkowego Ziemi stanowi odległość piramidy od bieguna N. Daje nam to: 6669, 3 km. W porównaniu z promieniem biegunowym Ziemi daje nam to różnicę aż 5 %. To znowu za dużo, jak na tak precyzyjną budowlę. Oczywiście odległość piramidy od środka Ziemi to jeszcze inna wartość, w końcu Ziemia nie jest idealną kulą i jej promień rośnie w kierunku równika.
Megabzdura.:Masa sarkofagu pomnożona przez 10 do piętnastej potęgi (biliard) jest równa masie Ziemi.
Wymiary zewnętrzne:
długość = 2, 28 m
szerokość = 0, 98 m
wysokość = 1, 05 m ----> objętość zewnętrzna: V = 2, 35 m³
Wymiary wewnętrzne:
długość = 1, 98 m
szerokość = 0, 68 m
głębokość = 0,87 m ----> objętość wnętrza (pojemność) V = 1, 17 m³
Różnica powyższych objętości da objętość użytego granitu: V = 1, 18 m³. Przy średniej gęstości skały granitowej ρ = 2 750 kg/m³ daje to masę sarkofagu wynoszącą: 3 245 kg
Po zastosowaniu się do "piramidalnych wskazówek" otrzymujemy "masę Ziemi": 3, 245 * 10^18 kg. Tymczasem masa Ziemi wynosi 5, 975 * 10^24 kg, czyli jest prawie 2 mln razy większa! To juz nie błąd. To wielbłąd...
Teraz obliczenia staną się trudniejsze, gdyż potrzebna jest tu większa precyzja. Zatem wymagane jest uwzględnienie wpływu niepewności pomiarowych użytych danych (np. wymiarów piramidy) na uzyskane wyniki rachunków. Margines błędu uzyskanych wyników obliczany był metodą różniczki zupełnej. Dla zrozumienia całego toku rozumowania nie jest wymagana znajomość tego, czym jest owa różniczka. Wystarczy wiedzieć, że określa ona nam dokładność uzyskanych wyników, czyli tak zwane „ ± ”.
Nieprawda. Trójkąt pitagorejski - trójkąt prostokątny, którego wszystkie boki mają długość wyrażoną liczbami całkowitymi. To, że tak skonstruowany trójkąt jest prostokątny, to nie ulega wątpliwościom, w końcu południki i równoleżniki przecinają się pod kątem prostym. Ale zajmijmy się szczegółami. Pomocny będzie rysunek:Południk przechodzący przez środek piramidy tworzy z równoleżnikiem przechodzącym przez piramidę Mykerinosa i z linią prostą łączącą te dwa punkty trójkąt pitagorejski.
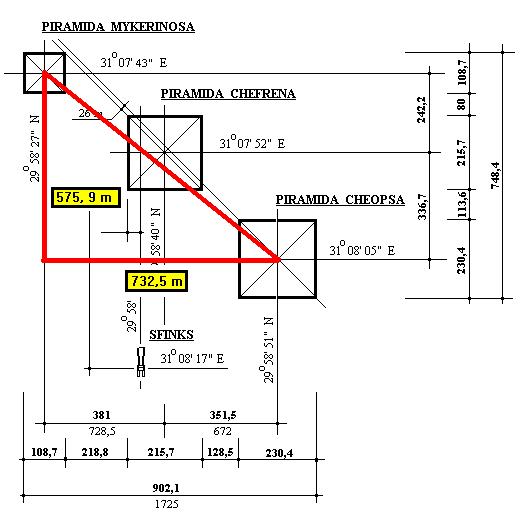
Uwzględniając powyższe niepewności otrzymujemy:
bok równoleżnikowy = 1099, 57 ± 1, 24 ł.e. (łokci egipskich)
bok południkowy = 1398, 57 ± 1, 52 ł.e.
Widać, że w granicy błędu mieści się kilka całkowitych wartości (to wymagane dla trójkąta pitagorejskiego):
bok równoleżnikowy = {1099, 1100}
bok południkowy = {1398, 1399, 1400}
Wartości wyglądają zachęcająco (szczególnie te okrągłe). Jednak musimy sprawdzić, czy dla wszystkich możliwych kombinacji boków prostopadłych trzeci bok także przyjmuje wartość całkowitą.
Po kolei (z tw. Pitagorasa):
dla (1099, 1398) --> trzeci bok: 1778, 26 ł.e.
dla (1099, 1399) --> trzeci bok: 1779, 04 ł.e.
dla (1099, 1400) --> trzeci bok: 1779, 83 ł.e.
dla (1100, 1398) --> trzeci bok: 1778, 88 ł.e.
dla (1100, 1399) --> trzeci bok: 1779, 66 ł.e.
dla (1100, 1400) --> trzeci bok: 1780, 44 ł.e.
Jak widać, żaden z wyników nie jest wynikiem całkowitym. Wynika z tego, że Egipcjanie nie zastosowali przy projekcie własności trójkąta pitagorejskiego.
Możliwym rozwiązaniem jest to, że w określaniu rozmieszczenia budowli na płaskowyżu Giza w kierunkach N-S i E-W Egipcjanie kierowali się okrągłymi wartościami długości (np. 1100 i 1400 łokci), ale cała reszta do już nadinterpretacja.
To przypadkowa zbieżność.:Obwód podstawy podzielony przez podwójną wysokość daje liczbę Pi=3,14169.
Bok N: 230, 251 ± 0, 216 m
Bok E: 230, 391 ± 0, 191 m
Bok S: 230, 454 ± 0, 127 m
Bok W: 230, 358 ± 0, 233 m
Wysokość piramidy: 146, 64 ± 0, 20 m
Obwód (Ob)= 921, 454 ± 0, 757 m
Podwojona wysokość (2h) = 293, 28 ± 0, 40 m
Szukany stosunek: Ob/2h = 3, 1419 ± 0, 0047 ≈ Π
Wartość otrzymana jest dość bliska Π (większa niż przyjmuje się to dla Egipcjan -> 3, 16), jednak warto zwrócić uwagę na spory błąd wyznaczenia tej wartości. Powoduje on, że możliwy wynik mieści się w dość szerokim zakresie między 3, 1372 a 3, 1466. Oczywiście te wartości są i tak zbyt dokładne, jak na to co wiemy o znajomości Π przez starożytnych Egipcjan.
Jednak wiele się wyjaśnia, gdy zaczniemy myśleć po staroegipsku i stosować długości miar tam używane: Przeliczenie średniej długości boku piramidy (230, 36 ± 0, 189 m) i wysokości na łokcie egipskie daje w wyniku (z uwzględnieniem wszelkich niepewności pomiarowych):
Bok piramidy: 439, 83 ± 0.78 ł.e.
Wysokość piramidy: 279, 98 ± 0, 65 ł.e.
Niemal oczywistym założeniem jest, że wymiary piramidy nie miały ułamkowych wartości, a wyrażały się w całkowitych liczbach. Jak widać, każdy z powyższych wyników zawiera w granicy błędu tylko jedną całkowitą wartość i ona na pewno wyraża pierwotną wartość danego wymiaru piramidy w łokciach egipskich. Mamy więc:
Bok piramidy: 440 łokci egipskich.
Wysokość piramidy: 280 łokci egipskich.
Ile wynosi stosunek Ob/2h w tym przypadku?
Ob/2h = 1760/560 = 3, 1428571.....
Ten wynik mieści się w granicach błędu wyniku otrzymanego w wyniku obliczeń przeprowadzonych na wielkościach wyrażonych w metrach. Doświadczony obserwator zauważy ponadto, że rezultat ten bardzo przypomina wartość Archimedesowego przybliżenia Π ≈ 22/7. Powiem więcej. Okazuje się ze to ten sam ułamek, czyli, że 1760/560 = 22/7!!! Czyżby Egipcjanie znali to przybliżenie!?
Można by było tak sądzić, lecz rozwiązanie jest inne i bardzo banalne, pod warunkiem, że zachowamy tok staroegipskiego myślenia i będziemy nadal używać ówczesnego systemu miar długości. Przypomnijmy więc, jak się on prezentuje w całej okazałości:
1 łokieć królewski = 7 dłoni = 28 palców.
Kolejną ważną rzeczą jest to, że Egipcjanie w czasach budowy piramid nie dysponowali miarą łukową (wynalezioną dopiero trochę później w Babilonii). Nie mogli więc konstruować dowolnych kątów (nachyleń) w swoich budowlach. Ich wartości były ściśle określone i wynikały z proporcji długości boków konstruowanego trójkąta. Były w pewnym sensie "produktem ubocznym" i nie określano ich wartości (my na szczęście możemy). Wyjaśnię powyższe stwierdzenia na przykładzie rysunkowym (oczywiście używamy staroegipskiego systemu miary):
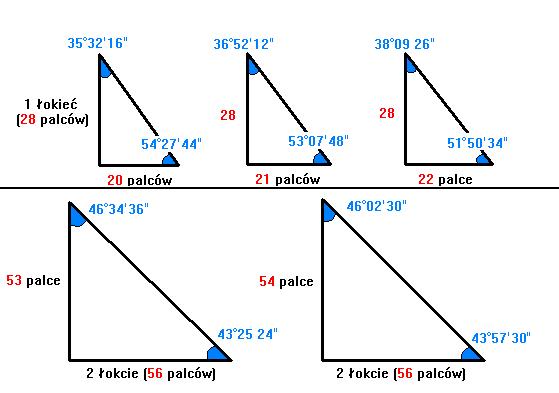
W zaawansowanej architekturze starożytnego Egiptu praktycznie nie spotkamy nigdzie pośrednich wartości kątów, a jedynie równe lub niemal równe wartościom (niewielkie odchylenia), które można zobaczyć na powyższym rysunku.
I tak dla WSZYSTKICH piramid, w których dokładnie określono kąt nachylenia można określić proporcję „p” między połową długości podstawy „a” a wysokością „h” (jak na trójkątach na rysunku). Każda konkretna proporcja odpowiada jednoznacznie odpowiedniej wartości kąta nachylenia ściany bocznej.
Poniżej zestawienie wartości proporcji dla egipskich piramid (większość proporcji przedstawiono na powyższym rysunku).
p = ½ a/h
Snofru (Medum, „Czarna”) -> 22/28
Snofru (Dahszur, „Łamana”) -> dół: 20/28 góra: 56/53
Snofru (Dahszur, „Czerwona”) -> 56/53
Chufu (Giza, „Wielka”)- > 22/28
Chefren (Giza) ->21/28
Menkaure (Giza) -> 28/35
Userkaf (Sakkara) -> 21/28
Neferirkare (Abusir) -> 21/28
Niussere (Abusir) -> 22/28
Unis (Sakkara) -> 28/42
Teti (Sakkara) -> 21/28
Pepi I (Sakkara Płd.) -> 21/28
Merenre (Sakkara Płd.) -> 21/28
Pepi II (Sakkara Płd.) -> 21/28
Amenemhat I (Liszt) -> 20/28
Senuseret I (Liszt) -> 24/28
Senuseret II (Lahun) -> 61/56
Senusertet III (Dahszur) -> 28/42
Amenemhat III (Dahszur) -> 18/28
Amenemhat III (Hawara) -> 28/32
Jak widać większość piramid budowana była wg kilku ustalonych proporcji (najczęściej 21/28). W absolutnej większości przypadków podane wyżej proporcje są niemal idealnie spełnione, tylko w kilku przypadkach maksymalny błąd wynosi ok. 0, 1% (można to porównać do ok. 15-centymetrowgo błędu wysokości dla piramidy o podstawie długości 200 m i wysokości 100 m). Zaiste „kosmiczna” jest precyzja WSZYSTKICH egipskich piramid.
Można zatem już stwierdzić skąd pochodzi ta „obecność” Π w wymiarach piramidy Chufu. Jest to tylko wynik przypadkowej korelacji wynikającej ze systemu miar używanego w starożytnym Egipcie. Okazuje się bowiem że stosunek 22/28 (odpowiada ilorazowi połowy długości podstawy i wysokości piramidy) wynosi Π/4 z dokładnością 0.04%.
A ponieważ:
Obwód (Ob) = 8* ½ a
Podwojona wysokość = 2*h
Proporcja dla p. Chufu = p ≈ Π/4
To: Ob/2h = 8 * ½ a/(2*h) ≈ 8/2*(Π/4) = Π
Na tym można zakończyć chyba to obalanie mitów związanych z Wielką Piramidą. Jest ona na pewno cudem architektury starożytnych Egipcjan, ale praktycznie takim samym jak pozostałe kilkadziesiąt budowli tego typu. To po prostu jedna z wielu egipskich piramid...
Dzięki za uwagę... oraz za dotarcie do końca ;-) .
EDIT: Poprawka trochę śmiesznie brzmiącej literówki.
EDIT2: Korekta przypadkowego błędu dla piramidy Menkaurego 28/25 -> 28/35












