CIĄG FIBONACCIEGO – ZŁOTY PODZIAŁ WSZECHŚWIATA

CIĄG FIBONACCIEGO fot.depositphotos.com
CIĄG FIBONACCIEGO
Co może być niezwykłego w ciągu liczb? Laicy powiedzą – że nic, bo co mogą przedstawiać poustawiane obok siebie cyferki.
Wtajemniczeni w świat nauki i matematyki – powiedzą, że wszystko.
W serii liczb ciągu Fibonacciego, być może rzeczywiście nie byłoby nic nadzwyczajnego, jednak pojawiają się one wszędzie wokół nas. W przyrodzie, w architekturze, inżynierii i sztuce, muzyce, fizyce, matematyce, a nawet w anatomii ludzkiego ciała…
Ciąg Fibonacciego, złota liczba i złoty podział
Leonardo Fibonacci żył w latach 1175-1250, był włoskim matematykiem pochodzącym z Pizy.
Uważał 0 za pierwszą liczbę naturalną, zajmował się rozkładem liczby na czynniki pierwsze. To dzięki niemu posługujemy się cyframi arabskimi i to właśnie on podał wzór określający kolejne wyrazy ciągu Fibonacciego.
Otóż w tym ciągu liczb naturalnych pierwsze dwa wyrazy ciągu są równe 1 a każdy następny wyraz (zwany liczbą Fibonacciego) powstaje jako suma dwóch poprzednich, czyli 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8 itd. aż do nieskończoności:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ...
Sam ciąg posiada kilka ciekawych właściwości.
Jeżeli podzielimy przez siebie dowolne, kolejne dwa wyrazy ciągu Fibonacciego, np. 987 : 610; 89 : 55 to stosunek tych liczb będzie równy zawsze tej samej liczbie, równej w przybliżeniu 1.618.
Im większe wyrazy ciągu podzielimy, tym dokładniejsze przybliżenie tej liczby uzyskamy. Liczbę tę nazywa się „złotą liczbą” i oznacza grecką literą φ (czyt. „fi”).
Stosunek tego podziału określa się również mianem „złotego podziału” lub „Boskiej proporcji”. Warto również wspomnieć o spirali Fibonacciego, szczególnym przypadku tzw. złotej spirali, której szerokość zwiększa się (lub zmniejsza) o 90° dokładnie φ razy (czyli o „złotą liczbę”).
Wygląda to tak:
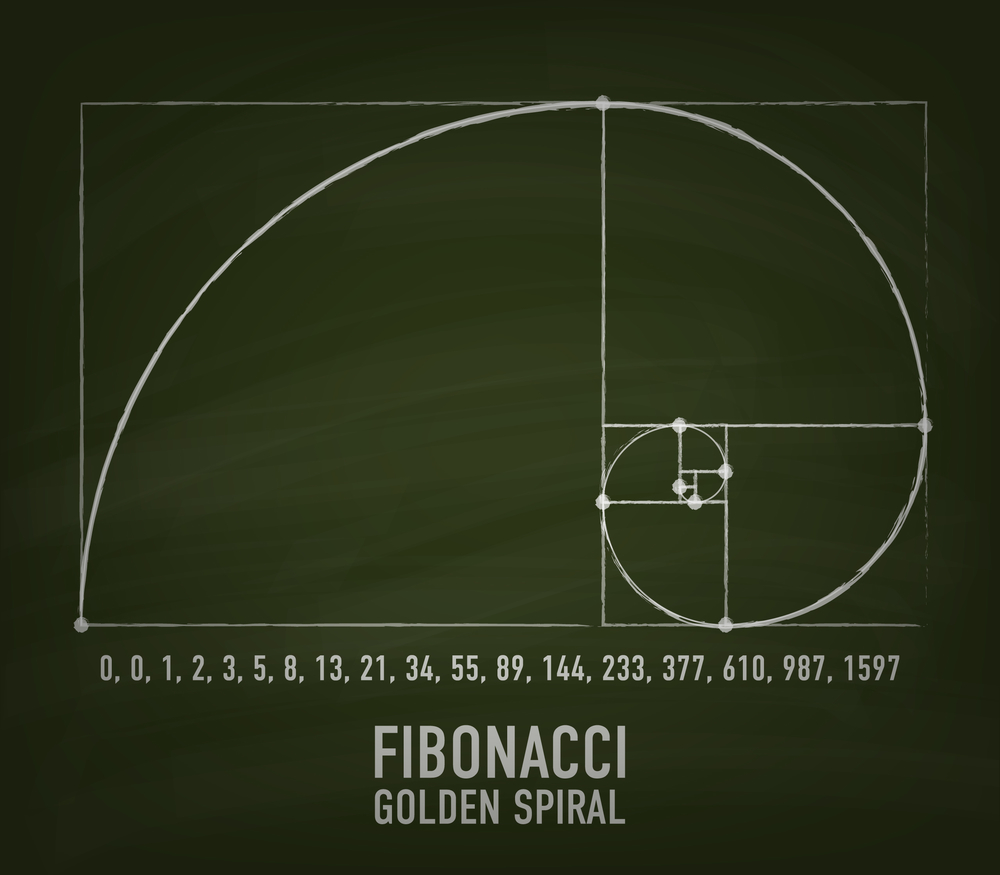
ZŁOTY PODZIAŁ fot.depositphotos.com
Jak już wcześniej wspomnieliśmy, ciąg Fibonacciego można odnaleźć wszędzie.
Teraz to udowodnimy.
Świat przyrody, a ciąg Fibonacciego
Zastanawialiście się kiedyś nad tym, dlaczego tak ciężko jest znaleźć czterolistną koniczynę?
Otóż sekret kryje się w matematyce.
W przytłaczającej większości optymalnie rozwinięty kwiat bez mutacji i deformacji, zawsze ma liczbę płatków będącą liczbą Fibonacciego (np. 1 płatek – lilia calla, 2 – wiloczmlecz, 3 – irys, 5 – dzika róża, 8 – ostróżka, 13 – nagietek, 21 – stokrotki, 34 – złocień).
Według zasad złotej proporcji odbywa się także cały proces wzrostu rośliny. Bez większego problemu złotą spiralę odnajdziemy w zdecydowanej większości roślin:

SŁONECZNIK I ZŁOTY PODZIAŁ fot.depositphotos.com
w słonecznikach, w szyszkach, stokrotkach, ananasach, brokułach, kalafiorach, kapuście itd.

KIWI I ZŁOTY PODZIAŁ fot.depositphotos.com
Zjawisko zwane spiralną filotaksją (ulistnieniem) cechuje bardzo wiele gatunków drzew. Myślimy tutaj o strukturze gałęzi układających się spiralnie wokół pnia.
Gdybyśmy ponumerowali gałęzie zgodnie z wysokością, na jakiej wyrastały to okaże się, że liczba gałęzi sąsiadujących pionowo jest liczbą Fibonacciego, a ponadto liczba gałęzi pomiędzy gałęziami sąsiadującymi pionowo również jest tą liczbą.
Zasada spiralnej filotaksji ma również swoje miejsce w świecie roślin, gdzie wyrastające liście wzajemnie się nie przysłaniają.
Co to daje?
W ten sposób rośliny mogą maksymalnie wykorzystywać posiadane miejsce, energię słoneczną oraz zebrać jak największą ilość deszczu.
Najlepszym przykładem spirali Fibonacciego w przyrodzie są muszle.

MUSZLA I ZŁOTY PODZIAŁ fot.depositphotos.com
Gdyby spojrzeć na muszlę łodzika (morskiego mięczaka) w przekroju, to można zauważyć, że ułożona jest spiralnie i zbudowana z szeregu komór, z których każda następna jest większa od poprzedniej dokładnie o tyle, ile wynosi wielkość tej poprzedniej.
Wynika to z faktu, że im są większe, tym szybciej rosną.
Ciąg Fibonacciego odnajdziemy także np. w budowie delfina. Poszczególne części jego ciała (oczy, płetwy, ogon) znajdują się w odległościach zgodnych z kolejnymi liczbami zbioru.
Dodatkowo średnica części ogonowej delfina znajduje się w złotej proporcji wobec jego górnej połowy ciała. W świecie przyrody zgodnie ze złotą proporcją formują się również huragany i galaktyki spiralne.
Ciało człowieka, a ciąg Fibonacciego
Najbliższe organizmowi ludzkiemu liczby ciągu Fibonacciego to 1,2 i 5.
Mamy dwie kończyny górne i dwie dolne, pięć zmysłów, trzy wypustki głowy (dwoje uszu i nos), trzy otwory głowy (dwoje oczu i usta) i pojedyncze organy.
Złoty podział i liczbę fi znajdziemy również w proporcjach naszego ciała. Co prawda proporcje te nie są tak idealnie i dokładnie zachowane, ale są na pewno bardzo zbliżone.
Dowód?
Weźmy na przykład stosunek wzrostu człowieka do odległości od stóp do pępka, który wynosi fi (1,618). Te same stosunki odległości równe liczbie fi, znajdziemy także w odległości np. od koniuszków palców do łokci – do odległości od łokcia do nadgarstka; od ramion do czubka głowy – do odległości od brody do czubka głowy; od pępka do czubka głowy – do odległości ramion do czubka głowy; od kolana do pępka – do odległości od kolana do stopy.
Mało?
Idźmy dalej: mamy 2 ręce, z których każda składa się z 5 palców. 8 palców składa się z 3 paliczków, a 2 kciuki składają się z 2 paliczków. Stosunek długości środkowego palca do małego równa się liczbie fi. Liczbę tę znajdziemy również w wyglądzie naszej twarzy.
fot.depositphotos.com
Przykładowo ma to miejsce w stosunku szerokości dwóch przednich zębów do ich wysokości; wysokości twarzy do jej szerokości, wysokości twarzy do odległości od brwi do podbródka; szerokości ust do szerokości podstawy nosa.
Złote proporcje zachowują nawet spirale naszego DNA. Cząsteczka DNA mierzy 34 jednostki długości na 21 jednostek szerokości dla każdego odcinka podwójnej spirali. Liczby te są oczywiście elementami ciągu Fibonacciego, a zależność między nimi jest równa liczbie fi.
Muzyka, sztuka i architektura, a ciąg Fibonacciego
Zasady ciągu Fibonacciego i złotej liczby możemy odnaleźć także w świecie muzyki. Zależności pomiędzy poszczególnymi dźwiękami w muzyce opierają się właśnie na matematycznych prawach harmonii, a dokładniej właśnie na liczbie fi.
Zakres dźwięków słyszalnych rozciąga się od 32 (największe piszczałki w organach) do 73700 (granie cykad) drgań na sekundę. Dźwięki zawarte w przedziale 60-33000 drgań mają charakter muzyczny. Odległości pomiędzy dwoma dźwiękami nazywane są interwałami.
Te najprzyjemniej brzmiące dla ucha powstają na podstawie liczby fi.
Zapis nutowy znanego kanonu D-Dur Pachelbela skonstruowany jest według liczb Fibonacciego a jego odzwierciedlenie można znaleźć w wielu współczesnych utworach muzycznych (np. Green Day – Basket Case, U2 – With or Without You, Bob Marley – Woman No Cry, The Beatles – Let It Be).
Ponadto większość z sonat Amadeusza Mozarta podzielona była na dwie części dokładnie z zachowaniem złotego podziału. Z zasady tej korzystał również Antonio Stradivarius podczas konstruowania swoich najlepszych wiolonczeli.
Mimo, że Fibonacci zauważył pewną prawidłowość dopiero w XIII w. to o złotej proporcji wiedzieli już w starożytnej Grecy. W oparciu o nią powstał ateński Partenon.
Zasadę tę wykorzystali również Egipcjanie przy tworzeniu piramid. Boczna ściana piramidy podzielona przez połowę podstawy daje nam w przybliżeniu liczbę fi.
Do tego dochodzi mnóstwo różnych przykładów ze sztuki m.in. obrazy: Mona Lisa, Ostatnia Wieczerza, Narodziny Wenus czy marmurowa rzeźba Wenus z Milo. Współcześnie zależności te można odnaleźć w logach znanych marek, jak np.
logo Apple, Toyoty, Pepsi, Google, BP, National Geographic.
Religia, a ciąg Fibonacciego
Niektórzy doszukują się występowania ciągu Fibonacciego również w kontekstach religijnych, chociaż wiele osób twierdzi, że są to poszukiwania wymuszone, działania na tzw. siłę. Jednak mimo wszystko przytoczmy kilka przykładów:
W mistycyzmie judaizmu, każdej literze w Biblii odpowiada cyfra, zatem istnieje możliwość zsumowania wartości odpowiednich wyrazów. Słowo „Ogród Eden” (qadam) po zamianie na cyfry daje 144; „Drzewo życia w ogrodzie Eden” – 233. Są to liczby Fibonacciego, które podzielone przez siebie dają fi.
Arka przymierza zrobiona z drzewa akacjowego. Jej długość miała wynosić 2,5 łokcia, a wysokość i szerokość 1,5 łokcia. Te liczby podzielone przez siebie dają przybliżenie fi.
Arka Noego – 50 łokci szerokości i 30 łokci wysokości, podzielone przez siebie również dają liczbę fi.
Pokoleń Izraela jest w Biblii 12. 12 podniesione do potęgi drugiej daje wynik 144 (liczbę Fibonacciego).
Być może doszukiwanie się wszędzie zasad i zależności ciągu Fibonacciego wydawać się może absurdem, to jednak fakty mówią same za siebie. Trzeba przyznać, że wiele rzeczy zachowuje zasady złotej proporcji, więc dlaczego mielibyśmy nie ufać matematyce?

















