Jakieś 1500 lat temu na terenie Indii dokonała się rewolucja, która wciąż wpływa na nasze życie. Indyjscy uczeni wymyślili pozycyjny system dziesiętny obejmujący pojęcie liczby zero – nie tylko jako symbolu, ale także jako wielkości, którą można wykorzystywać w obliczeniach. Właśnie tym systemem posługujemy się współcześnie.
Fot. Indigo Images
W Egipcie symbole służące do zapisu liczb pojawiły się ok. 3000 r. p.n.e. Mieszkańcy tego kraju wynaleźli matematykę w celu zaspokojenia konkretnych potrzeb. Pomiary terenu, podział ziemi po wylewie Nilu, planowanie kanałów irygacyjnych, piramid i świątyń, obliczanie ciężaru i podatków – wszystkie te zadania stały się tak skomplikowane, że ludzka pamięć i przekaz ustny przestały wystarczać.
Pojawiła się potrzeba zapisywania słów, poleceń, rachunków, tworzenia spisów inwentarza czy ludności. Grecy nazywali egipskie symbole grammata hieroglyphika („rzeźbione święte znaki”) i właśnie od tego określenia wywodzi się używana powszechnie nazwa „hieroglify”.
Początkowo hieroglify były piktogramami lub ideogramami (symbolami oznaczającymi słowo lub jakąś ideę), ale później przekształciły się w znaki oznaczające dźwięki (spółgłoski). Wykuwano je na kamiennych monumentach i zapisywano na papirusach, czyli arkuszach materiału przypominającego papier, które wytwarzano z rosnącej w delcie Nilu cibory papirusowej (wygląda jak trawa i osiąga nawet 3 m wysokości). W suchym klimacie Egiptu papirus można przechowywać bardzo długo, dzięki czemu do naszych czasów przetrwało wiele starych dokumentów.
Pierwszy w historii system dziesiętny
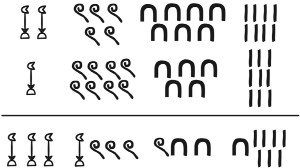
Od samego początku Egipcjanie potrafili zapisywać bardzo duże liczby, wykorzystując specjalne hieroglify na oznaczenie liczb 10, 100, 1000 i tak dalej aż do miliona.
Takie symbole stosowano, gdy tekst był pisany od lewej do prawej. Jeśli linię zawierającą liczbę należało czytać od prawej do lewej, powyższe symbole należało zapisać w lustrzanym odbiciu. Metoda tworzenia liczb z tych podstawowych symboli była bardzo prosta. Egipcjanie po prostu powtarzali poszczególne symbole odpowiednią ilość razy. Liczbę 2578 zapisaliby np. tak, jak pokazano poniżej:
Nie istniał symbol oznaczający zero, ponieważ nie był potrzebny do jednoznacznego zapisywania liczb. Obliczenia wykonywano, sprowadzając wszystko do dodawania. Wynika to stąd, że w stosowanym przez Egipcjan systemie liczbowym dodawanie dwóch liczb jest niezwykle proste. Aby zsumować np. liczby 2578 i 1859, wystarczy zebrać wszystkie jednakowe symbole i zastąpić każdą grupę dziesięciu symboli znakiem oznaczającym liczbę wyższego rzędu. To wystarczy, by bez trudu odczytać wynik: 4437.
Mnożenie dowolnej liczby przez 2 jest łatwe, ponieważ wystarczy jedynie dodać tę liczbę do siebie. Mnożenie przez 10 jest jeszcze prostsze, ponieważ sprowadza się do zastąpienia każdego symbolu w danej liczbie symbolem następnego wyższego rzędu. Mnożenie przez każdą inną liczbę sprowadzano w bardzo sprytny sposób do dodawania i mnożenia przez 2.
Liczby w Chinach
Egipcjanie, tak samo jak Grecy i Rzymianie, stosowali zapis liczb bazujący na zasadzie dodawania. Gdy w takim systemie chcemy zapisać jakąś liczbę, musimy jedynie powtórzyć odpowiednio wiele razy symbole oznaczające jeden, dziesięć, sto itd. Weźmy np. rzymską liczbę MCCCXXIII. Występuje w niej symbol oznaczający tysiąc, potem mamy trzykrotnie powtórzony znak oznaczający sto, następnie pojawiają się dwa symbole oznaczające dziesięć, a na końcu są trzy symbole o wartości 1 – wszystkie te znaki zostały powtórzone tyle razy, ile potrzeba, by przedstawić liczbę 1323. Tę samą liczbę zapisaną egipskimi hieroglifami pokazano na poniższej rycinie, która ilustruje „sumacyjną” metodę zapisu liczb.
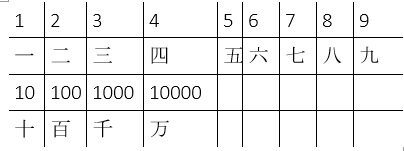
Około 3 tys. lat temu Chińczycy poszli o krok dalej i opracowali system zapisu wykorzystujący dodawanie i mnożenie. W jej współczesnej postaci, w tej metodzie wykorzystuje się symbole przedstawione w tabeli